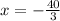List all real values of x such that f(x) = 0, if there are no such real x, type DNE as the answer. If there is more than one real x, give comma separated list (e.g. 1,2) X =

Question

asked Jun 1, 2023 112k views

1 Answer

Vijayeta · Answer 1 · 2023-06-05T05:31:32+0000

To answer this question, we can proceed as follows:

1. We can multiply by the least common multiple to both sides of the next equation:

$\begin{gathered} (-8)/(x-16)+(-1)/(x+17)=0 \\ \operatorname{lcm}(x-16,x+7)=(x-16)(x+17) \\ \end{gathered}$

2. Then we have:

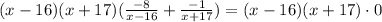
$(x-16)(x+17)((-8)/(x-16)+(-1)/(x+17))=(x-16)(x+17)\cdot0$
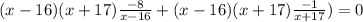
(x-16)(x+17)(-8)/(x-16)+(x-16)(x+17)(-1)/(x+17))=0

$((x-16))/((x-16))\cdot(x+17)\cdot(-8)+((x+17))/((x+17))\cdot(x-16)(-1)=0$
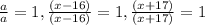
(a)/(a)=1,((x-16))/((x-16))=1,((x+17))/((x+17))=1

Then we have:

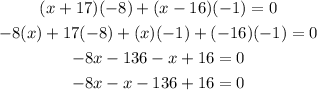
$\begin{gathered} (x+17)(-8)+(x-16)(-1)=0 \\ -8(x)+17(-8)+(x)(-1)+(-16)(-1)=0 \\ -8x-136-x+16=0 \\ -8x-x-136+16=0 \end{gathered}$

If we add the like terms, we have:

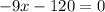
3. Adding 120 to both sides of the equation, and then dividing both sides of the equation by -9:

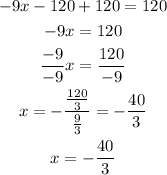
$\begin{gathered} -9x-120+120=120 \\ -9x=120 \\ (-9)/(-9)x=(120)/(-9) \\ x=-((120)/(3))/((9)/(3))=-(40)/(3) \\ x=-(40)/(3) \end{gathered}$

In summary, therefore, the value of x that makes f(x) = 0 is: