Question

Sarah blend coffee but she needs to prepare 150 pounds of blended coffee been selling for $4.33 per pound she plans to do this by blending together a high-quality beam costing $5.00 per pound and a cheaper being at $3.00 per pound to the nearest pound find how much high-quality coffee Bean and how much cheaper coffee then she should blend

Answer 1

Let x the number of pounds of the high-quality bean used in the mix, and y the number of pounds of the cheaper bean, then we can set the following system of equations:

`\begin{gathered} x+y=150 \\ 5x+3y=150\cdot4.33 \end{gathered}`

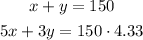
Solving the first equation for x, and substituting in the second equation we get:

`\begin{gathered} x=150-y \\ 5(150-y)+3y=150\cdot4.33 \\ 750-5y+3y=649.5 \\ 750-649.5=2y \\ y=(100.5)/(2) \\ y=50.25\approx50 \end{gathered}`

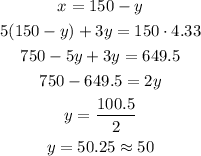
Therefore, x=150-50.25=99.75≈100.

Answer: 50 pounds of the cheap bean should be blended and 100 pounds of the high-quality bean should be blended.