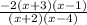Given:
The characteristics of rational function:
Vertical asymptotes at x = -2 and x = 4
x-intercepts at (-3,0) and (1,0).
horizontal asymptote at y = -2
The foem of rational function is,
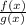
For the vertical asymtotes x = -2 and x = 4, That means denominator will have the terms,

For x intercept (-3,0) and (1,0) , the terms on the numerator is,
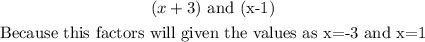
So, the rational function becomes,
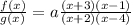
The horizontal asymtoes will describes the functions behaviour when x approaches to infinity.
So, a=-2.
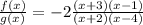
Answer: