y=2
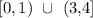
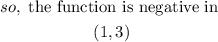
Step-by-step explanation
Step 1
The y -intercept of a graph is the point where the graph crosses the y -axis.
so , let's check the graph
therefore, the y-intercept is 2
Step 2
The positive regions of a function are those intervals where the function is above the x-axis. It is where the y-values are positive (not zero)
hence, the function is potive in ( in x axis)
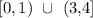
Step 3
negative region
The negative regions of a function are those intervals where the function is below the x-axis. It is where the y-values are negative (not zero).
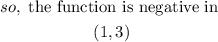
I hope this helps you