Question

The current of a river is 2 miles per hour. A boat travels to a point 8 miles upstream and back in 3 hours. What is the speed of the boat in still water?The speed of the boat in still water is.

Answer 1

Given:

The current of a river is 2 miles per hour. A boat travels to a point 8 miles upstream and back in 3 hours.

Required:

What is the speed of the boat in still water?

Step-by-step explanation:

A boat has to travel 8 miles against the current and 8 miles with the current.

Ustream(against the current) the boat's speed is:

speed in still water - current OR x - 2.

Downstream( with the current) the speed is:

speed in still water + current speed OR x + 2.

We know the distance

`=rate* time`

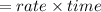
OR

`time=(distance)/(rate)`

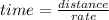
The total time is 3 hours

The time upstream + The time downstream = 3 hours

`\begin{gathered} \frac{distance\text{ }up}{rate\text{ }up}+\frac{the\text{ }distance\text{ }down}{rate\text{ }down}=3\text{ }hours \\ (8)/(x-2)+(8)/(x+2)=3 \\ \text{ we get,} \\ 3x^2-16x-12=0 \\ x=6,-(2)/(3) \end{gathered}`

Answer:

`\text{ The speed of boat in still water is }6\text{ miles per hour.}`