Question

Identify the figure by name, find the lateral area and the total surface area of the figure below. Be careful here because this figure may not be laying down on its base. Identify the figure first.

Answer 1

Name of the figure: Cone

Lateral Area: 770.66

Total Surface Area: 1084.82

Step-by-step explanation:

We identify the figure as a cone.

The lateral surface area of a cone is given by

`A_L=\pi r√(r^2+h^2)`

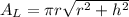
The total surface area includes the area of the base as well.

Since the area of the base is

`A_B=\pi r^2`

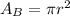
The total surface area then is

`A_(tot)=A_L+A_B=\pi r√(r^2+h^2)+\pi r^2`

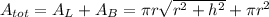
where

r = radius of the base

h = height of the cone.

Now in our case

r = 20/2 = 10

h = 22.4

therefore,

`A_L=\pi(10)√((10)^2+(22.4)^2)=770.66`
`A_B=\pi(10)^2=314.16`

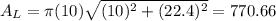
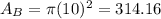
Therefore,

`A_(tot)=A_L+A_B=770.66+314.16`
`\Rightarrow\boxed{A_(tot)=1084.82.}`

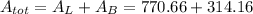
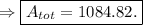
Hence, to summerise,

Name of the figure: Cone

Lateral Area: 770.66

Total Surface Area: 1084.82