ANSWER
• Distance when the motion began:, 4 cm
,
• Period: ,2π/3 sec
,
• Distance at t = 4.5 s:, 2.38 cm
Step-by-step explanation
When the motion begins, we usually set t = 0,

Hence, when the motion began, the pendulum was at 4 centimeters from the resting position.
The period of a sine or cosine function is given by 2π divided by the coefficient of t,

Hence, the period of the pendulum's motion is 2π/3 seconds.
Now, we have to find d(4.5) - remember to use your calculator in radians for this problem,
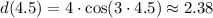
Hence, after 4.5 seconds the pendulum is at 2.38 centimeters from the resting position.