Given,
The angle of projection, θ_D=35.0°
The time of flight, T=45.0 s
The height, h=3.30 km=3300 m
A.
The time of flight of a projectile is given by,
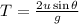
Where u is the initial velocity of the magma chunk and g is the acceleration due to gravity.
On substituting the known values,

Thus the initial speed of the magma chunk is 384.43 m/s
B. The horizontal distance of the flight of the magma chunk is given by,

Where u_x is the horizontal component of the initial velocity.
On substituting the known values,
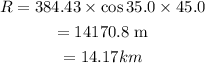
Thus the horizontal distance of the magma is 14.17 km