Question

A. Find the initial speed of the hot magma B. What horizontal distance (D in picture) did the hot magma travel?

Answer 1

Given,

The angle of projection, θ_D=35.0°

The time of flight, T=45.0 s

The height, h=3.30 km=3300 m

A.

The time of flight of a projectile is given by,

`T=(2u\sin \theta)/(g)`

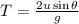
Where u is the initial velocity of the magma chunk and g is the acceleration due to gravity.

On substituting the known values,

`\begin{gathered} 45.0=(2* u*\sin 35.0\degree)/(9.8) \\ \Rightarrow u=(45.0*9.8)/(2*\sin 35.0\degree) \\ =384.43\text{ m/s} \end{gathered}`

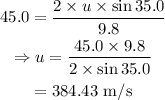
Thus the initial speed of the magma chunk is 384.43 m/s

B. The horizontal distance of the flight of the magma chunk is given by,

`\begin{gathered} R=u_xT \\ =u\cos \theta* T \end{gathered}`

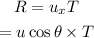
Where u_x is the horizontal component of the initial velocity.

On substituting the known values,

`\begin{gathered} R=384.43*\cos 35.0\degree*45.0 \\ =14170.8\text{ m} \\ =14.17km \end{gathered}`

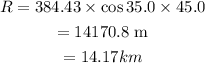
Thus the horizontal distance of the magma is 14.17 km