Question

A group fitness gym classifies it's fitness class attendees by class type and member status. The marketing team has gathered data from a random month, in which there were 2065 class attendees. The data is summarized in the table below. What is the probability that a class attendee is a non member of the gym and is attending a barre class or is a member of the gym and is attending a yoga class? Enter a fraction or round your answer to four decimal places if necessary

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the formula for probability

`Probability=\frac{number\text{ of required outcomes}}{number\text{ of total outcomes}}`

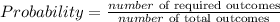
STEP 2: Find the probability that a class attendee is a non member of the gym and is attending a barre class

Using the table, the number of required outcomes is:

Therefore,

`P(non-member&barre)=(282)/(2065)`

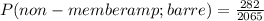
STEP 3: Find the probability that a class attendee is a member of the gym and is attending a yoga class

Using the table, the number of required outcomes is:

Therefore,

`P(member&yoga)=(209)/(2065)`

STEP 4: Find the probability that a class attendee is a non member of the gym and is attending a barre class or is a member of the gym and is attending a yoga class.

Using the addition law of probability, the probability either will be the sum of the two derived probabilities.

`(282)/(2065)+(209)/(2065)=(282+209)/(2065)=(491)/(2065)`

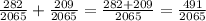
Hence, the probability that a class attendee is a non member of the gym and is attending a barre class or is a member of the gym and is attending a yoga class is 491/2065