Question

both circles have the same center. the circumference of the inner circle is 65.94 kilometers. what is the area of the shaded region?use 3.14 for ñ. write your answer as a whole number or a decimal rounded to the nearest tenth.

Answer 1

To determine the area of the shaded area, you have to determine the area of both circles and then calculate the difference between them.

First, using the circumference of the inner circle you can determine the length of its radius.

The formula of the circumference is:

`C=2\pi r`

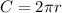
Write the formula for r:

`\begin{gathered} (C)/(2\pi)=(2\pi r)/(2\pi) \\ r=(C)/(2\pi) \end{gathered}`

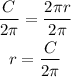
Use C=65.94km and π =3.14

`\begin{gathered} r=(C)/(2\pi) \\ r=(65.94)/(2\cdot3.14) \\ r=(65.94)/(6.28) \\ r=10.5km \end{gathered}`

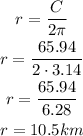
The radius of the inner circle is 10.5km.

Calculate the area of the inner circle:

`\begin{gathered} A=\pi r^2 \\ A=3.14\cdot(10.5)^2 \\ A=3.14\cdot110.25 \\ A=346.185km^2 \end{gathered}`

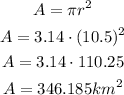
The next step is to determine the area of the outer circle.

- Calculate the length of the radius.

Since both circles have the same center, then the radius of the inner circle is part of the radius of the outer circle, the rest of the radius is equal to the distance between both circles. Add both lengths to determine the radius of the outer circle:

`\begin{gathered} r=10.5+24.7 \\ r=35.2km \end{gathered}`

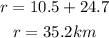
The radius of the outer circle is 35.2km

Calculate the area of the outer circle:

`\begin{gathered} A=\pi r^2 \\ A=3.14(35.2)^2 \\ A=3.14\cdot1239.04 \\ A=3890.5856km^2 \end{gathered}`

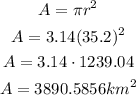
Once you have determined the area of both circles, calculate the difference between them, to determine the shaded area.

`3890.5856-346.185=3544.4006\cong3544.4km^2`

The shaded region has an area of 3544.40 square kilometers.