Question

Determine whether the following function is a polynomial function. If the function is a polynomial function, state its degree. If it is not, tell why not. Write the polynomial in standard form. Then identify the leading term and the constant term. F(x)= 8x^7−πx^5+1/5

Answer 1

`f(x)=8x^7-\pi x^5+(1)/(5)`

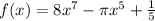
A function is a polynomial so long as there are no negative exponents in the variables.

As we can see in the terms above, there are no negative exponents in each variable. Hence, the given function is a polynomial function.

The degree of the function is the highest exponent. Hence, the degree is 7.

A polynomial in standard form is when the terms are arranged from highest to lowest exponent. As we can see, the terms are already arranged from highest to lowest degree. Hence, in standard form, it will still be f(x) = 8x⁷ - πx⁵ + 1/5.

The leading term is the term with the highest degree. It is 8x⁷.

The constant term is the term without a variable and that is 1/5.