Question

You are running a concession stand at a basketball game. You are selling hot dogs and sodas. Each hot dog costs $3 and eachsoda costs $2. At the end of the night you made a total of $78. You sold a total of 87 hot dogs and sodas combined. You mustreport the number of hot dogs sold and the number of sodas sold. How many hot dogs were sold and how many sodas were sold?

Answer 1

Let the number of hot dogs sold be represented by h and the number of sodas by s.

Each hot dog costs $3 and each soda costs $2. If $78 is made in total, we have the equation to be:

`3h+2s=78`

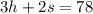
If a total of 87 hot dogs and sodas combined are sold, we have:

`h+s=87`

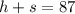
We can rewrite the second equation to give:

`s=87-h`

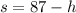
Substituting this value into the first equation, we get:

`\begin{gathered} 3h+2(87-h)=78 \\ 3h-2h+174=78 \\ h=78-174| \\ h=-96 \end{gathered}`

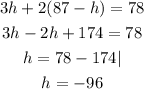
With the calculated value of h, we can get the value of s to be:

`\begin{gathered} s=87-(-96) \\ s=183 \end{gathered}`

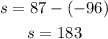
Since a negative value is gotten for the number of hot dogs, it does not represent a real-life scenario.