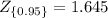Question

Dlay the tiles to the correct boxes. Not all tiles will be used.Jorge conducted a survey by asking 120 students whether they use a pencil to take notes. Of the students surveyed, 90 responded favorably.Which margin of error matches each confidence level for this situation?0.3380.2160.1020.2560.0650.077999695969096

Answer 1

The variable of interest is

X: number of students that use a pencil to take notes out of 120.

This variable has a binomial distribution with parameters n=120 and p. To calculate the confidence interval for the population proportion of students that use a pencil to take notes you have to use the approximation of the standard normal distribution with margin of error:

`Z_{\mleft\lbrace1-(\alpha)/(2)\mright\rbrace}\sqrt[]{\frac{p^(\prime)(1-p^(\prime))^{}}{n}}`

The sample proportion is the number of successes of the experiment divided the sample size, in this case the successes are the students that use a pencil so the sample proportion is:

p'=90/120=0.75

From the margin of error the only value modified will ve the Z value, so calculate the term under the square root first:

1-p'=1-0.75=0.25

`\sqrt[]{(0.75\cdot0.25)/(120)}=\frac{\sqrt[]{10}}{80}\cong0.0395`

Next, using the Z-table look for the corresponding values:

1) For 1-α= 99%=0.99

α=0.01

α/2=0.005

1-α/2=0.995

`Z_{\mleft\lbrace1-(\alpha)/(2)\mright\rbrace}=Z_(\mleft\lbrace0.995\mright\rbrace)=2.576`

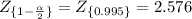
2) For 1-α=95%=0.95

α=0.05

α/2=0.025

1-α/2=0.975

`Z_(\mleft\lbrace0.975\mright\rbrace)=1.960`

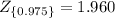
3) For 1-α=90%=0.90

α=0.1

α/2=0.05

1-α/2=0.95

`Z_(\mleft\lbrace0.95\mright\rbrace)=1.645`