Question

15.) The length of a rectangle is 6 feet more than four times the width.Setup and solve an equation to find the length and width if the areais 70 sq. ft. Use: LW = A(12 pts)

Answer 1

We are told to use L FOR LENGTH and B FOR BREADTH

We are also given that,

`\begin{gathered} l* w=A \\ lw=70----1 \end{gathered}`

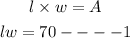
But we are given that the length of a rectangle is 6 feet more than four times the width. This implies that,

`l=6+4w-----2`

STEP 1: Create equation 3 from equation 1

`\begin{gathered} lw=70 \\ Therefore,l=(70)/(w) \end{gathered}`

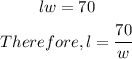
STEP 2: Substitute equation 3 into equation 2

`\begin{gathered} (70)/(w)=6+4w \\ \text{crossmultiply} \\ 70=w(6+4w) \\ 70=6w+4w^2 \\ 4w^2+6w-70=0 \\ Therefore \\ 2w^2+3w-35=0 \end{gathered}`

STEP 3: We solve the resulting quadratic equation to get the value of the width

`\begin{gathered} 2w^2+3w-35=0 \\ 2w^2+10w-7w-35=0 \\ 2w(w+5)-7(w+5)=0 \\ (2w-7)(w+5)=0 \\ \text{Therefore,} \\ 2w-7=0\text{ or w+5=0} \\ w=(7)/(2) \\ w=3.5\text{ or-5} \\ \end{gathered}`

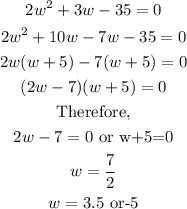
Since the width cannot be negative, the width of the rectangle is 3.5 feet

STEP 4: We solve for the length using equation 3

`\begin{gathered} l=(70)/(w) \\ l=(70)/(3.5) \\ l=20 \end{gathered}`

Therefore, the length of the rectangle is 20 feet