We are going to use the normal standard distribution to resolve this exercise, in that sense, finding the z value is necessary. Doing the calculations, we get
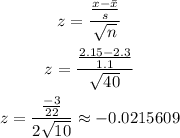
Now it only remains to calculate the probability, using a normal distribution calculator or a normal distribution table as follows
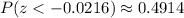
Thus, the probability that, for a sample of 40 college games to be played next week, the mean number of holding penalties will be 2.15 penalties per game or less is 0.4914