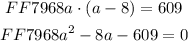The length of a rectangular plot is 8 feet more than its width.
The Area of the rectangular plot is 609 square feet.
If the length of the rectangular plot is a then the width will be (a - 8) since it is given that length is 8 feet more than its width.
Now recall that the area of rectangular shape is given by
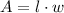
Where w is the width and l is the length.
We have
l = a
w = (a - 8)
A = 609
Substituting these values into the formula
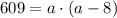
you can also write it as
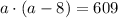
So option (B) is a correct option.
Now let us simplify the above equation
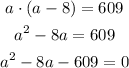
So option (E) is also a correct option.
Therefore, the following equations can be used to find the length (a) of the rectangular plot.