First, starting from the equation:
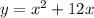
We should change every x for a y and every y for an x, so:
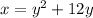
In the text, the first step was:
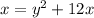
So, the first mistake was not to change the linear term 12x for 12y.
Another mistake was made from the following steps:
![\begin{gathered} y^2=-11x \\ y=\sqrt[]{-11x},x\ge0 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/cmguvdg4uza10l2c19fs0qs3c5c2gkfpiq.png)
The expression inside the square root must be greater or equal to 0, then:
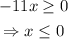
So, the second mistake was not to identify the domain of x correctly.
A third mistake is that the square root of y^2 is not y, it is |y|. So:
![\begin{gathered} y^2=-11x \\ \Rightarrow|y|=\sqrt[]{-11x} \\ \Rightarrow y=\pm\sqrt[]{-11x} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/6wsoaz2nisoh7q7btobzcrq4ry2w4c5zkt.png)