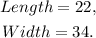Question

A rectangle has an area of 748 square inches. Its width is ten inches less than twice the length. Find the measures of the length and width of the rectangle.

Answer 1

To answer this question we will set and solve a system of equations.

Let l be the length (in inches) of the rectangle, and w be its width, then, since the rectangle has an area of 748 square inches and Its width is ten inches less than twice the length, then we can set the following system of equations:

`\begin{gathered} w*l=748, \\ w=2l-10. \end{gathered}`

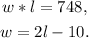
Substituting the second equation in the first one we get:

`(2l-10)*l=748.`

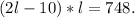
Applying the distributive property we get:

`2l^2-10l=748.`

Subtracting 748 from the above equation we get:

`\begin{gathered} 2l^2-10l-748=748-748, \\ 2l^2-10l-748=0. \end{gathered}`

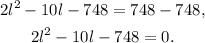
Dividing the above equation by 2 we get:

`\begin{gathered} (2l^2-10l-748)/(2)=(0)/(2), \\ l^2-5l-374=0. \end{gathered}`

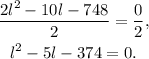
Now, notice that:

`\begin{gathered} 17-22=-5, \\ 17*(-22)=-374. \end{gathered}`

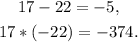
Then:

`l^2-5l-374=(l+17)(l-22).`

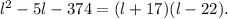
Therefore:

`l^2-5l-478=0\text{ if and only if }l=22\text{ or }l=-17.`

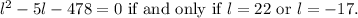
Since l is the length of a rectangle, then l>0, therefore l=22.

Substituting l=22 in the second equation we get:

`w=2*22-10=44-10=34.`

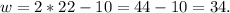
Answer:

`\begin{gathered} Length=22, \\ Width=34. \end{gathered}`