Question

I need to know which is the best estimate for rabbit population after 5 years

Answer 1

`\text{ B: 800 rabbits}`

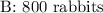
Step-by-step explanation:

Here, we want to estimate the rabbit population after 5 years

From the question, there was an approximate increase in the rabbit population by 150 (from 150 to 300) in a space of 2 years

Let us have an exponential relationship for this:

`P=I.a^t`

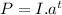
Let us get the value of t

P is the current population at 300

I is the initial

a is ?

t is the number of years which is 2

Mathematically, we have it that:

`\begin{gathered} 300\text{ =150 }* a^2 \\ a^2\text{ = 2} \\ a\text{ = }\sqrt[]{2} \end{gathered}`

Now, for the 5 years tenor, we substitute 5 for t

We have that as:

`\begin{gathered} P\text{ = 150}*\text{ (}\sqrt[]{2})^5 \\ P\text{ = 849} \end{gathered}`

From the option, we have an approximate value of 800 rabbits