3.2 s
Step-by-step explanation
Step 1
Let
![\begin{gathered} \text{aceleration}=a=9.8\text{ }(m)/(s^2) \\ \text{ Initial sp}eed=v_0=23.016\text{ }(m)/(s) \\ \text{time}=\text{ t=unknown} \\ \text{ final sp}eed=195\text{ }\frac{\operatorname{km}}{\text{h}} \end{gathered}]()
to solve this we need to use the free fall formula:
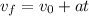
in order to use that formula, we need to have the same measure unit on each data, we will use meters, seconds, so we need to convert hte final velocity from KM/h into m/s
so

now, we can replace the data into the formula:
Step 2
replace

therefore, the answer is
3.2 seconds