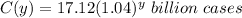Solution:
The volume of the cases in 2001 is given below as
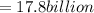
The percentage increase from 2000 is given below as
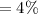
The exponential function is given below as
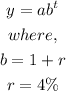
By substituting the values, we will have
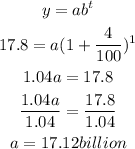
Hence,
The final answer is YES, THE EXPONENTIAL MODEL FUNCTION IS APPROPRIATE
Therefore,
The exponential model after y years will be