Question

Factor the polynomial f(x) = x ^ 3 + 2x ^ 2 - 4x - 8 and find all its real zeros using the Zero Product Property .

Answer 1

Given the polynomial;

`f(x)=x^3+2x^2-4x-8`

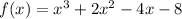
We shall begin by factorizing in groups.

We take

`\begin{gathered} x^3+2x^2 \\ \text{Factor out x}^2 \\ x^2(x+2) \end{gathered}`

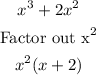
We now take the other part which is;

`\begin{gathered} -4x-8 \\ \text{Factor out -4} \\ -4(x+2) \end{gathered}`

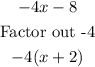
We now have;

`x^2(x+2)-4(x+2)`

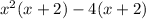
We can regroup the factors and we have;

`(x^2-4)(x+2)`

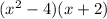
Next step, we factorize;

`(x^2-4)`

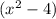
We can apply the difference of squares formula, which is;

`(x^2-y^2)=(x+y)(x-y)`

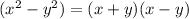
We now have;

`\begin{gathered} (x^2-4)=(x^2-2^2) \\ (x^2-2^2)=(x+2)(x-2) \end{gathered}`

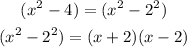
Therefore, the polynomial after being completely factorized becomes;

`f(x)=(x+2)(x-2)(x+2)`

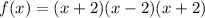
The zero product property states that;

`\begin{gathered} \text{If} \\ a* b=0 \\ \text{Then;} \\ a=0,b=0 \end{gathered}`

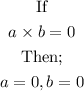
Therefore, the polynomial woul now become;

`(x+2)(x-2)(x+2)=0`

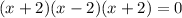
We can now solve;

`\begin{gathered} x+2=0,x=-2 \\ x-2=0,x=2 \end{gathered}`
`\begin{gathered} f(x)=(x+2)(x-2)(x+2) \\ x=-2,x=2 \end{gathered}`

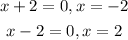
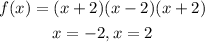
Also, when we have the factors as;

`(x+2)(x-2)(x+2)`

This can be re-arranged to become;

`\begin{gathered} (x-2)(x+2)(x+2) \\ (x-2)(x+2)^2 \\ \text{Note that }(x+2)\text{ occurs twice} \end{gathered}`

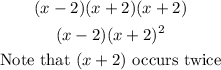
ANSWER:

`f(x)=(x-2)(x+2)^2`