Question

The demand function for a product is p= 200 -10q where p is the price in dollars when q units are demanded. The revenue function for the product is R (q) = q(200-10q) find the level of production that maximizes the total revenue and determine the revenue q= units R = $

Answer 1

From the statement of the problem we know that:

• the demand function is:

`p=200-10q,`

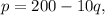
where p is the price in dollars when q units are demanded,

• the revenue function for the product is:

`R(q)=q\cdot p=q(200-10q)=200q-10q^2.`

We must find the level of production q that maximizes the total revenue R.

We maximize the function R(q), by equalling to zero its first derivative:

`(dR)/(dq)=200-10\cdot2q=0\Rightarrow20q=200\Rightarrow q=(200)/(20)=10.`

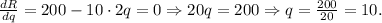
The level of production that maximizes the total revenue is q = 10 units.

The maximum value of the revenue is:

`R(q=10)=10\cdot(200-10\cdot10)=1000.`

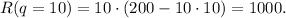
Answer

• q = 10 units,

,

• R = $1000.