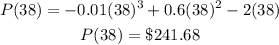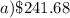
a) To maximize the profit, we'll need to find the Profit function. We know that each item is sold for $10 so the Revenue is R(q)= 10q the profit will be found by subtracting the cost from the Revenue:
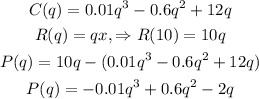
Now, to maximize it we'll need to take the derivative of this Profit function and equate it to zero, applying the power rule like this :
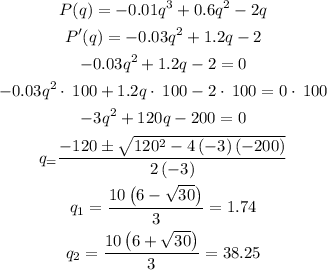
Let's take the second derivative test to get to know which are we going to use:
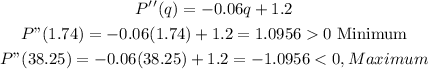
So the Maximum profit is obtained if we sell it for 38 units (rounding off to the nearest whole), which yields: