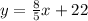Question

I just need the equation and I want to do it before me daughter thanks you

Answer 1

Let's begin by identifying key information given to us:

We have the best line of fit that is a straight line.

The equation of a straight line is given by the equation: y = mx + b

We will pick two coordinates that lie on the straight line to form the equation:

`\begin{gathered} (x_1,y_1)=(5,30) \\ (x_2,y_2)=(30,70) \end{gathered}`

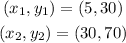
We will proceed to calculate the slope of the equation using the coordinates above. We have:

`\begin{gathered} m=(\Delta y)/(\Delta x)=(y_2-y_1)/(x_2-x_1)=(70-30)/(30-5) \\ m=(40)/(25)=(8)/(5) \\ \therefore m=(8)/(5) \end{gathered}`

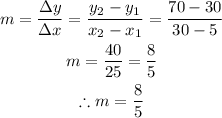
Since slope (m) = 8/5, the equation of the line becomes:

`\begin{gathered} y=mx+b \\ m=(8)/(5) \\ \Rightarrow y=(8)/(5)x+b \end{gathered}`

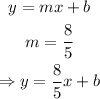
The y-intercept (where the straight line touches the y-axis) of the graph equals 22: b = 22

Therefore, the equation of the straight line thus becomes:

`y=(8)/(5)x+22`