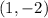DEFINITIONS AND FORMULAS
The equation of a straight line can be written in the slope-intercept form to be:

where m is the slope and b is the y-intercept.
The formula to calculate the slope is given to be:

SOLUTION
Table 1: Two points can be picked from the table as shown below
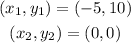
Therefore, the slope is calculated to be:
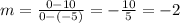
The y-intercept is the value on the y-axis when the x-axis is 0. Therefore:
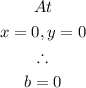
Therefore, the equation of the first table is:
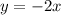
Table 2: Two points can be picked from the table as shown below
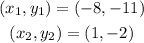
Therefore, the slope is calculated to be:
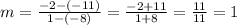
Therefore, the equation of the line is:
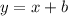
To find the value of b, we need to substitute one of the ordered pairs in the table into the equation and solve for b:
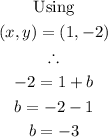
Therefore, the equation of the second table is:
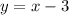
To get the solution to the system of equations, we can plot the graphs of the equations. This is shown below:
The solution to the system is the point where both graphs intersect.
Therefore, the solution to the system is:
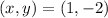
ANSWERS
The equation of the first system is:
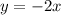
The equation of the second system is:
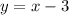
The solution to the system is: