Question

The drawing shows two boxes resting on frictionless ramps. One bax is relatively light and sits on a steep ramp. The other box isheavier and rests on a ramp that is less steep. The boxes are released from rest at A and allowed to slide down the ramps. The twoboxes have masses of 14 and 38 kg. If A and B are 6.0 and 0.5 m, respectively, above the ground, determine the speed of (a) the lighter box and (b) the heavier box when each reaches B. (c) What is the ratio of the kinetic energy of the heavier box to that of the lighter box at B?

Answer 1

We are asked to determine the velocity of the boxes at B. To do that we will consider the energy at A and the energy at B.

Since the velocity at A is zero this means that the only type of energy is gravitational potential energy. At B we have kinetic energy and gravitational potential energy. Since energy is conserved we set both energy equal:

`mgh_A=(1)/(2)mv_B^2+mgh_B`

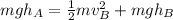
We can cancel put the mass:

`gh_A=(1)/(2)v_B^2+gh_B`

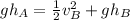
Now, we solve for the velocity at B. First, we multiply both sides by 2:

`2gh_A=v_B^2+2gh_B`

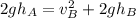
Now, we subtract "2gh" from both sides:

`2gh_A-2gh_B=v_B^2`

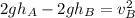
Now, we take "2g" as a common factor:

`2g(h_A-h_B)=v_B^2`

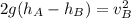
Now, we take the square root to both sides:

`√(2g(h_A-h_B))=v_B`

Now, we substitute the values:

`\sqrt{2(9.8(m)/(s^2))(6m-0.5m)}=v_B`

Solving the operations:

`10.38(m)/(s)=v_B`

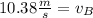
Since the velocity does not depend on the mass or the inclination of the ramp the velocity for both blocks is the same.

Now, we determine the kinetic energy using the following formula:

`K=(1)/(2)mv^2`

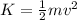
Now, we determine the kinetic energy of the heavier box:

`K_(heavier)=(1)/(2)(38kg)(10.38(m)/(s))^2`

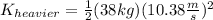
Solving the operations:

`K_(heavier)=2047.14J`

Now, we determine the kinetic energy for the lighter box:

`K_(lighter)=(1)/(2)(14kg)(10.38(m)/(s))^2=754.21J`

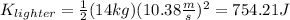
Now, we determine the ratio:

`(K_(heavier))/(K_(lighter))=(2047.14)/(754.21)=2.71`

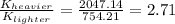
therefore, the ratio is 2.71