Step-by-step explanation:
Let 'x' be the amount of 80% alcohol solution needed.
The amount of alcohol in the 30% alcohol solution is:
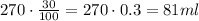
The amount of alcohol in the 80% alcohol solution is:
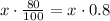
The sum of these amounts is the amount of alcohol resulting of the mixture. We need the 35% of the final mixture be alcohol. This is:

So we have to solve the following equation for x:
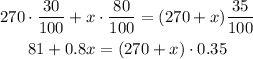
Solving we have:
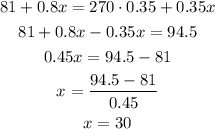
The total amount of the 35% alcohol solution obtained is:
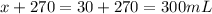
Answer:
You will need 30 mL of the 80% alcohol solution.
The total amount of the 35% solution you'll obtain is 300mL