Hello there. To solve this question, we have to remember some properties about limits.
Given the following limit:
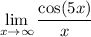
We want to determine its value.
For this, we'll use the "sandwich" theorem, that is also called as the squeeze theorem.
Notice that
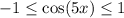
Hence dividing both sides of the equation by a factor of x, we'll get
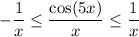
Taking the limit as x goes to infinity (and of course this works for x very large), it wouldn't work if we were to determine the value at 0.
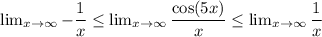
The left and right hand side limits are equal to zero, hence
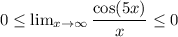
And this is precisely the value of this limit:
