Answer:
The earthquake in North Cascades was about 63 times greater than the earthquake that happened near Woodburn Oregon in 1993
Explanations:
Given the magnitude, M, of an earthquake in relation to the seismic waves, W, modeled by the equation below;
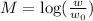
If in 1872, the North Cascades suffered its largest known earthquake of magnitude 7.4, hence;
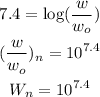
Similarly for the earthquake that happened near Woodburn Oregon in 1993 which had a magnitude of 5.6, the ratio of the seismic wave that occur is expressed as:
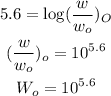
Taking the ratios of the seismic wave will give:
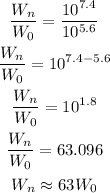
This shows that the earthquake in North Cascades was about 63 times greater than the earthquake that happened near Woodburn Oregon in 1993