areaThe Lateral area of a Triangular prism is the area of the sides
The sides of the prism are two Rectangles.
We need to calculate the Hypotenues side of right angle triangle
![\begin{gathered} \text{hyp}^2=\text{adj}^2+\text{opp}^2 \\ \text{hyp}^2=12^2+3^2 \\ =144+9 \\ =153 \\ \text{hyp}=\sqrt[]{153}=3\sqrt[]{17} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/55zn8qn4u7m41t0o0cj51u5gi6o8wc3hc9.png)
The lateral Area is given as
Area the side excluding the area of the base
![\begin{gathered} \text{atrea of rectangle =l}* b \\ =(8*3\sqrt[]{17})+(8*12) \\ =24\sqrt[]{17}+96 \\ =194.95\operatorname{cm}^2 \end{gathered}]()
The surface area of the prism is the area of all the surface
Area of 2Rectangles+Area of 2 Triangles +Area of the Base rectangle
The area of the two rectangles is given as LxB
![\begin{gathered} \text{area of rectangle =(8}*3\sqrt[]{17})+(8*12) \\ =194.95\operatorname{cm}^2 \end{gathered}]()
The are of the Two Triangles is given as
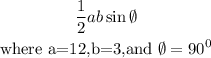
![\begin{gathered} (1)/(2)*3*12*\sin 90^0 \\ =3*6=18cm^2 \\ \text{where sin90=1} \\ \text{the area of the two triangle is } \\ 18*2=36\operatorname{cm}^2 \end{gathered}]()