Recall that a critical point is a point in the domain of the function where the function is either not differentiable or the derivative is equal to zero.
1) The first derivative of the given function is:
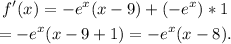
Notice that f'(x) is the product of two continuous functions, then it is continuous.
Setting f'(x)=0 we get:

Then:
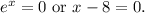
We know that for all x real number:
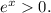
Then:
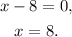
Answer 1:
Option A) The critical point(s) is(are) x=8.
2) Now, notice that f''(x) is the derivative of f'(x), then:
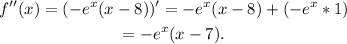
Now, evaluating f''(x) at x=8 we get:
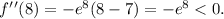
Using the second derivative test we get that f(x) reaches a local maximum.
Answer 2:
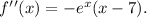
f(x) reaches a local maximum at x=8.