Solution:
A ship travels 6km south, and then 8km west.
The diagrammtic expression is shown below
To find θ, we will apply SOHCATOA
Given
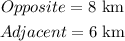
Applying the tan formula
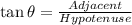
Substitute the values of the side lengths into the formula above
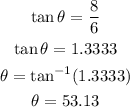
The bearing of the ship from the source to destination will be
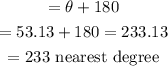
Hence, the answer is 233° (nearest degree)