Question

Two weather tracking stations are on the equator 159 miles apart. A weather balloon is located on a bearing of N 38°E from the western station and on a bearing of N 14°E from the eastern station. How far is the balloon from the western station?

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Redraw the given triangle

STEP 2: Write the needed measures

`\begin{gathered} A=90-38=52^(\circ)----Right\text{ angle} \\ B=90^(\circ)+14^(\circ)=104^(\circ) \\ C=180-104^(\circ)-52^(\circ)=24^(\circ) \\ c=159miles \\ b=required\text{ side} \end{gathered}`

STEP 3: State the Sine rule

`(\sin A)/(a)=(\sin B)/(b)=(\sin C)/(c)`

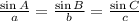
STEP 4: Substitute the known measures into the formula

`\begin{gathered} (\sin B)/(b)=(\sin C)/(c) \\ (\sin104)/(b)=(\sin24)/(159) \\ Cros\text{s multiply} \\ b\cdot\sin24=159\cdot\sin104 \\ b=(159\cdot\sin104)/(\sin24) \\ b=(154.2770205)/(0.406736643)=379.3044544 \\ b\approx379.3\text{ miles} \end{gathered}`

Hence, the balloon is approximately 379.3 miles away from the western station.