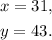Question

Hi there I need help with this question, please make it simple I am in year 9

Answer 1

To answer this question, we will set and solve a system of linear equations.

Let x be the length of route X, and y be the length of route Y. In one week Cyd drove route X five times and route Y three times, therefore, we can set the following equation:

`5x+3y=284.`

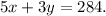
In another week, she drove route x twice and route y seven times, therefore:

`2x+7y=363.`

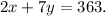
Solving the second equation for x, we get:

`\begin{gathered} 2x=363-7y, \\ x=(363-7y)/(2)\text{.} \end{gathered}`

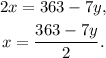
Substituting the above result, in the first equation, we get:

`5((363-7y)/(2))+3y=284.`

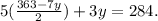
Solving the above equation for y, we get:

`\begin{gathered} 5((363)/(2))-5((7)/(2))y+3y=284, \\ (1815)/(2)-(35)/(2)y+3y=284, \\ 1815-35y+6y=568, \\ -29y=-1247, \\ y=43. \end{gathered}`

Now, we substitute y=43 in x=(363-7y)/2 and get:

`x=(363-7\cdot43)/(2)=31.`

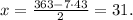
Answer: x is the length of route X, and y is the length of route Y.

`\begin{gathered} x=31, \\ y=43. \end{gathered}`