By the law of radioactive decay, the amount of a certain radioactive isotope as a function of time is given by
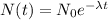
Where N_0 represents the initial amount of the substance, N represents the amount of the substance given a time t, and lambda is the decay constant.
This isotope that has leaked, started with an amount N_0, and after 300 days remained only 11% of it, which means that
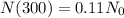
If we evaluate 300 in our function, we're going to have
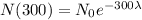
If we compare those two results, we have
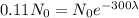
Dividing both sides by the initial amount.
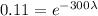
Solving for lambda, we have

The decay rate and the half life of a isotope are related by the following formula
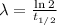
Where t_(1/2) is the half life of the isotope.
Using our value for lambda, we have

The half life of this substance is approximately 94 days.