Answer:
The volume of the solids are;
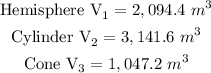
We can observe that ;
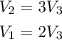
The volume of the cylinder is three times the volume of the cone and the volume of the hemisphere is twice the volume of the cone.
Step-by-step explanation:
Given the three solids in the attached image.
We want to find the volume of each.
The hemisphere;

Substituting the values;
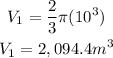
The cylinder;
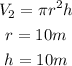
substituting the values
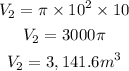
The cone;

substituting the values;

Therefore, the volume of the solids are;
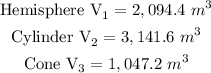
we can observe that ;
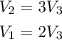
The volume of the cylinder is three times the volume of the cone and the volume of the hemisphere is twice the volume of the cone.