Question

An object is dropped from the top of Pittsburgh's USX Towers, which is 841 feet tall. The height of the object after t seconds is given by the function h(t) = 841 - 16t2. To the nearest whole number, estimate when the object hits the ground. _____ seconds. please use desmos to get your answer

Answer 1

In order to estimate when the object hits the ground, let's use h(t) = 0 in the equation and calculate the value of t:

`\begin{gathered} h(t)=841-16t^2 \\ 0=841-16t^2^{} \\ 16t^2=841 \\ t^2=(841)/(16) \\ t=(29)/(4)=7.25 \end{gathered}`

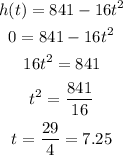
Therefore the time for the object to hit the ground is 7.25 seconds.

Using Desmos to find the graphic solution, we have:

The graph has a y-value of zero for a horizontal value of 7.25, therefore h(7.25) = 0

(The quadrants II and III are not useful since time can't be negative).