Answer:
a)
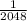
b)
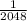
Step-by-step explanation:
a) Given:
Flipping eleven fair coins
To find:
The theoretical probability that all eleven will come up tails
Recall the below probability formula;
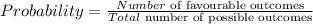
If one fair coin is flipped, the total number of possible outcomes is 2 (HT) and the probability of obtaining a tail will 1/2.
So if eleven coins are flipped, the probability that all eleven will come up tails will be;
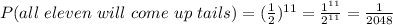
So the probability that all eleven will come up tails is 1/2048
b) The probability that the first toss is head is;
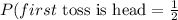
The probability that the next ten are tails will be;
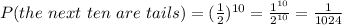
Therefore the probability that the first toss is head AND the next ten are tails will be;
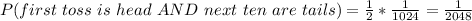
So the probability that the first toss is head AND the next ten are tails is 1/2048