Question

Find the difference quotient for the quadratic functionf(x) = 2x^2 + 5x - 8

Answer 1

Given the function:

`f\mleft(x\mright)=2x^2+5x-8`

We will find the difference quotient for the given function

We will use the following formula:

`(f(x+h)-f(x))/(h),h\\e0`

so, we will find f(x+h) then find the differnce of f(x+h) and f(x)

`\begin{gathered} f(x+h)=2(x+h)^2+5(x+h)-8 \\ \end{gathered}`
`f(x+h)-f(x)=2(x+h)^2+5(x+h)-8-(2x^2+5x-8)`

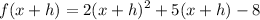
Expand then simplify

`\begin{gathered} f(x+h)-f(x) \\ =2(x^2+2hx+h^2)+5x+5h-8-2x^2-5x+8 \\ =2x^2+4hx+2h^2+5x+5h-2x^2-5x \\ =(2x^2-2x^2)+(5x-5x)+4hx+5h+2h^2 \\ =4hx+5h+2h^2 \end{gathered}`

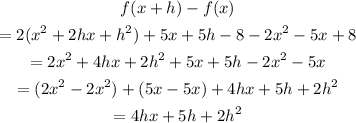
Now, divide the result by (h)

`\begin{gathered} (f(x+h)-f(x))/(h)=(4hx+5h+2h^2)/(h) \\ \\ =(h(4x+5+2h))/(h)=4x+5+2h \end{gathered}`

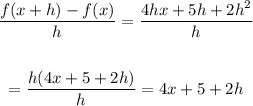
So, the answer will be:

The the difference quotient = 4x + 5 + 2h