Question

9. The weekly salaries of teachers in one state are normally distributed with a mean of$1850 and a standard deviation of $75. What is the amount of money thatseparatesa) bottom 3% of these teachersb) top 15% of these teachers

Answer 1

(a) To find the values that separates the bottom 3%, we can use a z-score table or z-score calculator. The distribution we have is not in terms of z, so after we find the z-score such that the data separates the bottom 3%, we have to convert it to x value using:

`z=(x-\mu)/(\sigma)`

Where μ is the mean and σ is the standard deviation.

Consulting a table for z-scores, we can see that the z-score value that separates the bottom 3% is approximately -1.88, that is:

`P(z<-1.88)\cong0.03`

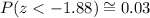
Thus, we can use this value of z to calculate x:

`\begin{gathered} z=(x-\mu)/(\sigma) \\ x=z\sigma+\mu \\ x=-1.88\cdot75+1850 \\ x=-141+1850 \\ x=1709 \end{gathered}`

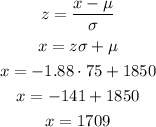
So, the value that separates the bottom 3% is $1709, that is, approximately 3% have a salary less than $1709.

(b) Here we do similarly, but we consult the value for top 15%, but usually we need to check the values below, not up, so we can check insteade, the value that separates the bottom 85%, which will be the same as the one that separates the top 15%.

Consulting a table for z-scores, we can see that the z-score value that separates the bottom 85% is approximately 1.04, that is:

`\begin{gathered} P(z<1.04)=0.85 \\ P(z>1.04)=0.15 \end{gathered}`

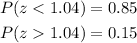
Now, we just convert it to x:

`\begin{gathered} x=1.04\cdot75+1850 \\ x=78+1850 \\ x=1928 \end{gathered}`

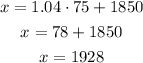
So, the value that separates the top 15% is $1928, that is, approximately 15% have a salary greater than $1928.