Answer:
(a) Symmetric to the x - axis: ( 7, 8)
(b) Symmetric to the y - axis: (-7, -8)
(c) Symmetric to the origin: (-7, 8)
Step-by-step explanation:
(a)
A point (a,b) is said to be symmetric with respect to the x-axis when
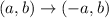
therefore, for the point ( 7, -8) a point that is symmetric with respect to the x-axis is
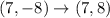
Hence, a point symmetric to (7, -8) with respect to the x-axis is (7,8).
(b)
A point (a,b) is said to be symmetric with respect to the y-axis when
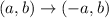
therefore, for the point ( 7, -8) a point that is symmetric with respect to the y-axis is
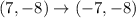
Hence, a point symmetric to (7, -8) with respect to the y-axis is (-7,-8).
(c).
A point (a,b) is said to be symmetric with respect to the origin when
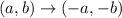
therefore, for the point (7, -8), a point symmetric with respect to the origin is

Hence, a point symmetric to (7, -8) with respect to the origin is (-7,8).
The graph of the three points is given below: