Given the question in the question tab, we can get the annual percentage yield by following these steps:
Step 1:
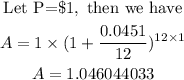
So the annual percentage yield becomes
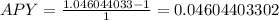
Since APY is given in percentage, we convert to percentage, i.e,
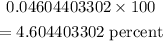
Hence, annual percentage yield is 4.60 percent to two decimal places.