We are asked to graph the following function:

Before sketching the graph we will simplify the function. To do that we will use the following property of exponentials:

Applying the property we get:
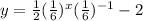
Now we use the following property:
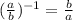
Applying the property we get:
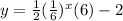
Simplifying we get:
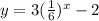
Now, we will graph the function. To do that we will need to determine three points of the graph.
The first point we will determine it by setting x = 0, to determine the y-intercept:

Therefore, the point:
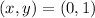
is part of the graph. Now, we will set x = 1:
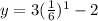
Solving the operations:
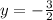
Therefore, the point:
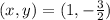
Now, we will determine the horizontal asymptote. To do that we need to analyze what happens when x goes to infinity. As the values of "x" get larger and larger the value of:
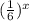
will tend to zero, since would have a large number of products of 1/6 and as the denominator grows the numerator will stay as 1 and therefore, the fraction will go to zero, therefore, the asymptote is:
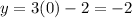
Now, we plot the points and the asymptote, we get the following graph:
The direction of the graph is due to the fact that the function is a decay function.