Question

3. Find mZS.(5r + 2)°P (10x - 3)(7x-11)ºR(136 - 31)(&r - 19° 2TSbananicho boloSind the

Answer 1

`m\measuredangle s=151`

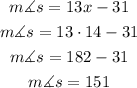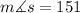
Step-by-step explanation

Step 1

In every convex polygon, the sum of the measure of the interior angles is given by the expression SUM = 180 ° (n - 2) where n is the number of sides.

Let

number of sides:

PQ

QR

RS

ST

TP

5 sides

number of sides:5

Step 2

apply the equation

`\begin{gathered} \text{Sum =180(n-2)} \\ \text{Sum}=180(5-2) \\ \text{Sum}=180\cdot3 \\ \text{Sum}=540\text{ degr}ees \end{gathered}`

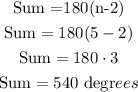
Step 3

now, in the graph we have these angles

`\begin{gathered} (5x+2) \\ (7x-11) \\ (13x-31) \\ (8x-19) \\ (10x-3) \end{gathered}`

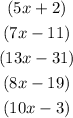
it means

`\begin{gathered} \text{Sum}=\text{ (5x+2)+(7x-11)+(13x-31)+(8x-19)+(10x-3)} \\ \text{add similar terms} \\ \text{Sum}=x(5+7+13+8+10)+(2-11-31-19-3) \\ \text{Sum}=43x-62 \end{gathered}`

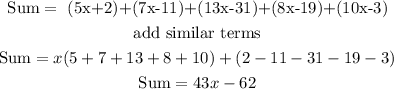
Finally, replace

Step 4

`\begin{gathered} Sum=\text{ 540 degre}es\text{ } \\ \text{and} \\ \text{Sum}=43x-62 \\ \text{then} \\ 540=43x-62 \\ \text{add 62 in both sides} \\ 540+62=43x-62+62 \\ 602=43x \\ \text{divide both sides by 43} \\ (602)/(43)=(43x)/(43) \\ x=14 \end{gathered}`

Step 5

replace the value of x in ms to find it

`\begin{gathered} m\measuredangle s=13x-31 \\ m\measuredangle s=13\cdot14-31 \\ m\measuredangle s=182-31 \\ m\measuredangle s=151 \end{gathered}`