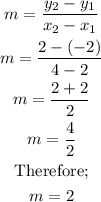Question

Determine thefor each of the following functions. Be careful!12Xyxy3162051046105247106288107329103.Xуу112- 222423466478105111014

Answer 1

In order to determine the slope (rate of change) for a given function, we shall use the following formula;

`m=(y_2-y_1)/(x_2-x_1)`

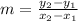
(1) Starting with the first set of ordered pairs, we have the coordinates as follows;

`\begin{gathered} (x_1,y_1)=(3,16) \\ (x_2,y_2)=(4,20) \end{gathered}`

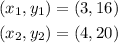
Therefore, the slope is derived as;

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ m=(20-16)/(4-3) \\ m=(4)/(1) \\ \text{Therefore, } \\ m=4 \end{gathered}`

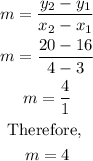
(2) For the set of ordered pairs given;

`\begin{gathered} (x_1,y_1_{})=(5,10) \\ (x_2,y_2)=(6,10) \end{gathered}`

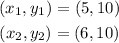
Therefore the slope is derived as;

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ m=(10-10)/(6-5) \\ m=(0)/(1) \\ \text{Therefore;} \\ m=0 \end{gathered}`

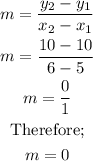
(3) For the set of ordered pairs given;

`\begin{gathered} (x_1,y_1)=(1,1) \\ (x_2,y_2)=(2,2) \\ (x_3,y_3)=(3,4) \\ (x_4,y_4)=(4,7) \end{gathered}`

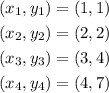
Therefore the slope is derived as;

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ m=(2-1)/(2-1) \\ m=(1)/(1) \\ \text{Therefore;} \\ m=1 \end{gathered}`

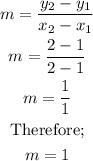
Note however, that if we use any two sets of coordinates, the value of the slope must alway be the same. We shall now use the third and second ordered pair.

`\begin{gathered} m=(y_3-y_2)/(x_3-x_2) \\ m=(4-2)/(3-2) \\ m=(2)/(1) \\ \text{Therefore;} \\ m=2 \end{gathered}`

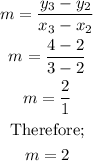
As you can observe, the value of the slope is different along varying points, which means these coordinates do not belong to a straight line. If we used the coordinates for the fourth and third points, the slope would be equal to 3 (and not 1 OR 2). Therefore, the slope for this function is not defined.

(4) For the set of ordered pairs given;

`\begin{gathered} (x_1,y_1)=(2,-2) \\ (x_2,y_2)=(4,2) \end{gathered}`

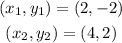
Therefore, the slope is derived as;

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ m=(2-(-2))/(4-2) \\ m=(2+2)/(2) \\ m=(4)/(2) \\ \text{Therefore;} \\ m=2 \end{gathered}`