Question

Determine if the two line are parallel, perpendicular or neither 1. Line A contains the points (0, 3) and (3,1)Line B contains the points (-1, 4) and (-7,-5)

Answer 1

Explanation:

Let us call

a = slope of line A

b = slope of line B

then the two lines are perpendicular if

`a=-(1)/(b)`

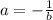
Now, what is the value of a, the slope of line A?

We find it by using the two points that lie on line A: (0, 3) and (3, 1).

The slope of line A is

`\text{slope a}=\frac{\text{rise}}{\text{run}}=(3-1)/(0-3)=(2)/(-3)`

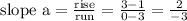
Hence,

`a=-(2)/(3)`

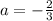
Now what is the value of b, the slope of line B?

We find it using the two points that lie on B: (-1, 4) and (-7, 5).

`\text{slope b=}\frac{rise}{\text{run}}=(4-5)/(-1-(-7))`

`=(-1)/(-1+7)=-(1)/(6)`

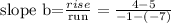
Hence,

`\text{slope b = -}(1)/(6)`

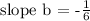
Now is it true that a = -1 / b?

Let us see.

`-(1)/(b)=-(1)/(-1/6)=6`

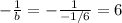
which is not equal to - 2/3!

Since the condition a = -1/b is not met, the two lines are not perpendicular.