Question

You want to make a conical candle using 15 in. of wax. If the candle's height is twice its diameter, what radius and height should it have, to the nearest tenth?

Answer 1

We know that the candle will have 15 cubic inches of wax, this is the volume.

Now, if the candle's height is twice its diameter, then we express

`h=2d`

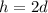
Additionally, the volume of a cone is

`V=(1)/(3)(\pi)r^2h`

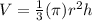
Where pi=3.14. Also, we know that the radius is half the diameter, so we'll use the following expression

`h=2\cdot2r=4r`

Replacing all, we have

`\begin{gathered} 15=(1)/(3)(3.14)r^2\cdot4r \\ (45)/(3.14)=4r^3 \\ 4r^3=14.3 \\ r=\sqrt[3]{(14.3)/(4)} \\ r\approx1.53 \end{gathered}`

The radius should be 1.5 inches long.

Then, we find the height

`\begin{gathered} h\approx4(1.53) \\ h\approx6.12 \end{gathered}`

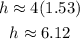
The height should be 6.1 inches long.