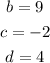Question

312 + 21 - 21- 2:2 – 21 + 12212 + 255 + 63612 + 71 - 49If a = 1, find the values of b, c, and d that make the given expression equivalent to the expression below.ai + >CD + db=and d =CE

Answer 1

Given the expression :

`(3x^2+2x-21)/(-2x^2-2x+12)\cdot(2x^2+25x+63)/(6x^2+7x-49)`

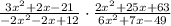
so, at first , we need to factor each function of the expression :

`\begin{gathered} 3x^2+2x-21=(3x-7)(x+3) \\ -2x^2-2x+12=-2(x^2+x-6)=-2(x+3)(x-2) \end{gathered}`

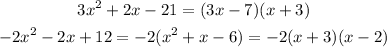
And for the second fraction:

`\begin{gathered} 2x^2+25x+63=(2x+7)(x+9) \\ 6x^2+7x-49=(2x+7)(3x-7) \end{gathered}`

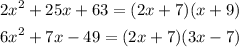
So, writing the given expression using the factors :

The result will be :

`((3x-7)(x+3))/(-2(x+3)(x-2))\cdot((2x+7)(x+9))/((2x+7)(3x-7))`

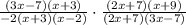
Cross the similar factors :

As you can see, at the numerator : (3x-7) , (x+3) and (2x+7) are similar with the same factors in the denominator

so, after crossing the similar factors, the result will be :

`(x+9)/(-2(x-2))=(x+9)/(-2x+4)`

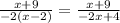
The result is similar to :

`(ax+b)/(cx+d)`

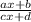
So, as a = 1 , the values of the other variables will be :

`\begin{gathered} b=9 \\ c=-2 \\ d=4 \end{gathered}`